Support Vector Machine algorithm with mathematical derivation and numpy implementation
Machine learning(ML) is
an application of artificial intelligence (AI) ,where the system learns
automatically and improves the performance from experience without being
explicitly programmed.



Regression and Classification are types of ML algorithms.
Classification
is a type of supervised learning. It
predicts the class of the given data point.
Support Vector Machine (SVM)
Classifier:
SVM is a
supervised Machine Learning Algorithm used predominantly for Non-linear Classification
type of data modelling. It is used in a variety of applications such as
face detection, handwriting recognition and classification of emails.
It
employs the concept of using a hyper-plane to separate the data sets into
classes. If there are ‘n’ features,’n-1’ dimension hyper-plane will be used
i.e. for a 2-D space hyper-plane will be a line ,in case of a 3-D space
hyper-plane will be a plane and so on. Support
Vectors are the co-ordinates of individual observation.
Hyper-plane selection:
Following
are the conditions based on which the right hyper-plane will be selected:
1. If there are a
number of hyper-planes, the one which well-segregates the feature is selected.
2. Margin:
Distance
of the hyper-plane from the nearest data point is called a Margin. Maximizing
the margin helps to find the right hyper-plane. If we select hyper-plane with
low-margin then there will be high chance of misclassification, so selecting
the hyper-plane with high distance will increase the robustness.


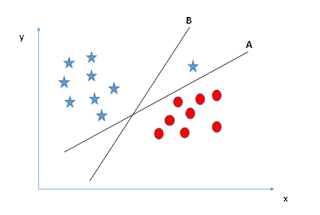
3. Prior to classifying based on the Margin, SVM
selects the hyper-plane which classifies the data points accurately.In this case the right hyper-plane is A though hyper-plane B has high margin.
4. SVM
has a feature to ignore Outliers and choose the hyper-plane with maximum
margin.
Soft Margin is a technique used primarily
with Non-linear data to tolerate the one or few misclassified points.
Applying
soft margin, tries to balance the trade-off between finding a line that
maximizes the margin and minimizes the misclassification.


The
amount of tolerance (soft) is an important user-defined parameter for SVM. In
Scikit learn,it is represented as the penalty term ’C’. Higher the value of C ,
SVM gets more penalty when it makes misclassification , narrowing down the
margin by considering only a few support vectors for decision-making.
Hyper-parameter tuning with various values can be done (will be discussed later
in the chapter) to find the best value of C for the model.
5. Hyper-plane
for Non-linear data is selected by introducing a new feature Z, which is
calculated as follows,

where N
is the number of chosen features for the analysis.- Z will always have a positive value as it is the squared sum of the features.
- Data points closer to origin will have a smaller value of Z whereas value of Z will be higher for data points away from the origin.


SVM uses
the Kernel Trick which takes the
existing features, applies transformation and returns new features which are
then used for finding the decision boundary .Kernel parameter selection is very
helpful in Non-linear classification problems where complex data transformation
techniques are used to convert the non-separable data to separable data based
on the input features. Multiple choice of kernels like
‘linear’,’polynomial’,Radial Basis function(rbf) are available.Polynomial
and rbf are best suited for Non-linear data.
Gamma is an important parameter in
rbf, which controls the influence of the new features on the decision
boundary.Higher the value of gamma will create impact on the adjacent data
points.Lower the better.we can choose the Kernel and gamma values best fitting
our model using the hyper-parameter tuning(discussed later in the section).
SVM Mathematical Derivation:
Hyper-plane
equation for Linear data:
In case
of 2-D space, the hyper-plane to separate the classes will be a line.
Considering
the line equation,
y=ax+b
mx+c-y=0
Let us
consider X=x,y and W as (a,-1),then the above equation becomes,
W.X+c=0
Most of
the real-time scenarios will have non-linearly separable data. In this case a
new feature will be introduced (discussed earlier in point 5 of hyper-plane
selection) to classify the data points.
Any hyper-plane can be written as the set of
points x satisfying w⋅x+b=0 --(1)

We have found the formula to calculate the
margin. Minimum the norm(||w||) maximum will be the Margin (m).
Let’s explain
margin calculation with an example:
Orthogonal projection of a vector and Dot product of the vectors are the concepts used to compute the
distance of a data point from the hyper-plane.
To find
distance between the vector w(2,1) which is normal to the hyper-plane and a(3,4),we
consider a projection vector P from w:
SVM Implementation:
Hyper-Parameter
Tuning:
There
are number of parameters in SVC which help to improve the performance of the
data model.
Kernel, Gamma and C are the most important of them.
Cross validation is a method for evaluating
models. To find the optimal hyper-parameters, we take a set of candidate hyper
parameters, train models for all of these and compare their fitness via cross
validation. Finally we select the hyper-parameters that gave the best CV score.
To
choose the best values for these parameters the following approaches are used.
GridsearchCV is commonly used as an
approach to hyper-parameter tuning that will methodically build and evaluate a
model for each combination of algorithm parameters specified in a grid.(code
available in implementation section)
RandomSearchCV
uses a random set of
hyper-parameters. In contrast to GridSearchCV, not all parameter values are
tried out, but rather a fixed number of parameter settings is sampled from the
specified distributions. The number of parameter settings that are tried is
given by n_iter.
SVM implementation in Python:
Let us
develop the SVC model for the famous Iris dataset using numpy and scikit learn.
#import the
necessary packages:
import pandas as pd
from sklearn.model_selection
import train_test_split
from sklearn.metrics import
accuracy_score
from sklearn.model_selection
import GridSearchCV
from sklearn.svm import SVC
from sklearn.metrics import
classification_report, confusion_matrix
#Read Iris dataset
from the folder
data=pd.read_csv('IRIS.csv')
#Train_test data
split:
data_train,data_test=train_test_split(data,test_size=0.2,random_state=0)
print('Train data
set:',data_train.shape)
print('Test data
set:',data_test.shape)
O/p:
Train data set: (120, 5)
Test data set: (30, 5)
#Splitting the
train and test data into inputs and output column
data_train_x=data_train.drop(columns='species',axis=1)
data_train_y=data_train['species']
data_test_x=data_test.drop(columns='species',axis=1)
data_test_y=data_test['species']
#Hyperparameter
tuning using GridSearchCV:
param_grid = {'C': [0.1,1, 10,
100], 'gamma': [1,0.1,0.01,0.001],'kernel': ['rbf', 'poly', 'sigmoid']}
grid =
GridSearchCV(SVC(),param_grid,refit=True,verbose=2)
grid.fit(data_train_x,data_train_y)
O/p:
Fitting 3 folds for each of 48 candidates, totalling 144 fits
[CV] C=0.1, gamma=1, kernel=rbf ......................................
[CV] ....................... C=0.1, gamma=1, kernel=rbf, total= 0.0s
[CV] C=0.1, gamma=1, kernel=rbf ......................................
[CV] ....................... C=0.1, gamma=1, kernel=rbf, total= 0.0s
[CV] C=0.1, gamma=1, kernel=rbf ......................................
[CV] ....................... C=0.1, gamma=1, kernel=rbf, total= 0.0s
[CV] C=0.1, gamma=1, kernel=poly .....................................
[CV] ...................... C=0.1, gamma=1, kernel=poly, total= 0.0s
#Display the best
choice of estimators to tune the model
print(grid.best_estimator_)
O/p:
SVC(C=1, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma=1, kernel='poly',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
Implementation using Numpy:
For best
understanding of the SVC implementation using Numpy we consider only two
features:
Sepal
Length and Sepal Width
class SVM():
def
__init__(self,kernel="rbf",polyconst=1,gamma=10,degree=2):
self.kernel = kernel
self.polyconst = float(1)
self.gamma = float(gamma)
self.degree = degree
self.kf = {
"linear":self.linear,
"rbf":self.rbf,
"poly":self.polynomial
}
self._support_vectors = None
self._alphas = None
self.intercept = None
self._n_support = None
self.weights = None
self._support_labels = None
self._indices = None
def linear(self,x,y):
return np.dot(x.T,y)
def polynomial(self,x,y):
return (np.dot(x.T,y) +
self.polyconst)**self.degree
def rbf(self,x,y):
return
np.exp(-1.0*self.gamma*np.dot(np.subtract(x,y).T,np.subtract(x,y)))
def transform(self,X):
K = np.zeros([X.shape[0],X.shape[0]])
for i in range(X.shape[0]):
for j in range(X.shape[0]):
K[i,j] =
self.kf[self.kernel](X[i],X[j])
return K
def fit(self,data,labels):
num_data, num_features = data.shape
labels = labels.astype(np.double)
K = self.transform(data)
P =
cvxopt.matrix(np.outer(labels,labels)*K)
q = cvxopt.matrix(np.ones(num_data)*-1)
A = cvxopt.matrix(labels,(1,num_data))
b = cvxopt.matrix(0.0)
G = cvxopt.matrix(np.diag(np.ones(num_data)
* -1))
h = cvxopt.matrix(np.zeros(num_data))
alphas = np.ravel(cvxopt.solvers.qp(P,
q, G, h, A, b)['x'])
is_sv = alphas>1e-5
self._support_vectors = data[is_sv]
self._n_support = np.sum(is_sv)
self._alphas = alphas[is_sv]
self._support_labels = labels[is_sv]
self._indices =
np.arange(num_data)[is_sv]
self.intercept = 0
for i in range(self._alphas.shape[0]):
self.intercept +=
self._support_labels[i]
self.intercept -=
np.sum(self._alphas*self._support_labels*K[self._indices[i],is_sv])
self.intercept /=
self._alphas.shape[0]
self.weights=np.sum(data*labels.reshape(num_data,1)*self._alphas.reshape(num_data,1),
axis=0,keepdims=True)
if self.kernel ==
"linear"
else
None
def signum(self,X):
return
np.where(X>0,1,-1)
def project(self,X):
if self.kernel=="linear":
score =
np.dot(X,self.weights)+self.intercept
else:
score = np.zeros(X.shape[0])
for i in range(X.shape[0]):
s = 0
for alpha,label,sv in
zip(self._alphas,self._support_labels,self._support_vectors):
s +=
alpha*label*self.kf[self.kernel](X[i],sv)
score[i] = s
score = score + self.intercept
return score
def predict(self,X):
return self.signum(self.project(X))
model =
SVM(kernel="rbf",gamma=3)
model.fit(data_train_x,data_train_y)
predictions =
model.predict(data_test_x)
Implementation using Scikit
Learn:
modelsvc= SVC(C=1,
cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma=1, kernel='poly',
max_iter=-1, probability=False, random_state=None, shrinking=True,tol=0.001,
verbose=False)
# Fit the Train
data to build the model
modelsvc.fit(data_train_x,data_train_y)
#Predict the
accuracy using the test data
predict=modelsvc.predict(data_test_x)
Accuracy=accuracy_score(data_test_y,predict)
print(Accuracy)
O/p:
1.0
References:



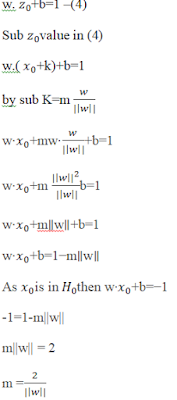




SVM implementation in Python is impressive and throws nimberous insights to Python students.
ReplyDeleteWell done. Keep the good working going.
ReplyDeleteFantastic article post.Really thank you! Awesome.
ReplyDeletemachine learning course in hyderabad
best machine learning course in india